第一节换元法
例1.计算
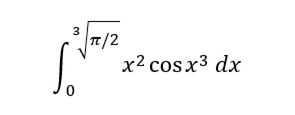
有人可能会说:直接微积分第二定理就搞定了!
不,这积分不太简单,因为我们找不到它的反导数
为了简便的计算这个定积分,我们可以先算这个不定积分

然后令t=x^3 ,则不定积分变成
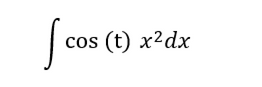
然后就可以计算了?不!你有没有发现,这里有两个自变量? ( t和x)
为了统一,我们必须换掉一个量,很明显我们要换掉x^2 dx ,换成以a dt的形式(a为常数)
好在我们令t=x^3了,那么就有dt/dx=3x^2
这样,就有
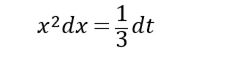
即
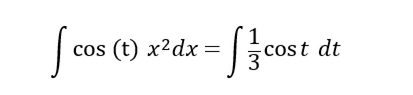
现在即可计算这个不定积分了
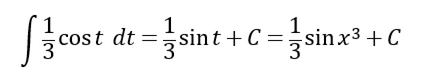
我们现在找到了反导数(即sinx^3/3 ) ,所以我们把结果代到定积分,然后使用微积分第二定理,得到
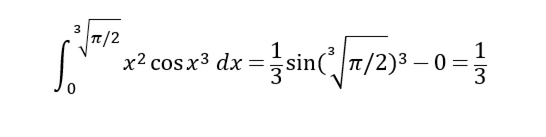
例2.计算
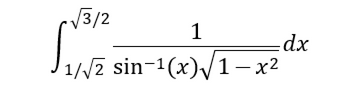
看起来好像无从下手啊,但实际上我们有
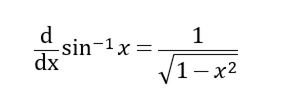
令t=sin^-1x,则
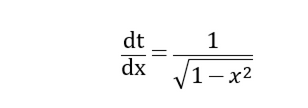
也就是
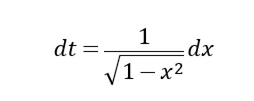
按照上一个例子,我们先计算不定积分以找到反导数
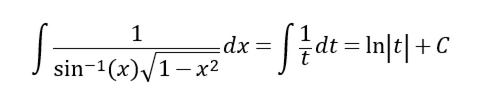
我们找到了反导数
然后把视线转到定积分,注意一点,在这里我们的做法与上一一个例子不太相同
我们把积分上限和下限用妹表示,也就是把x= 1/√2和x=√3/2分别代入t=sin^-1x,就得到
t=π/3和t=π/3
也就是
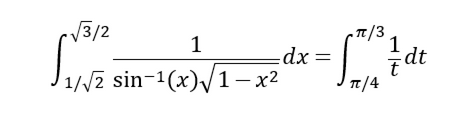
求得
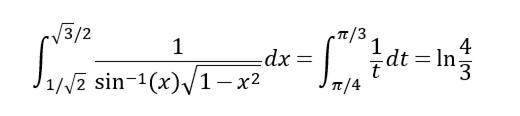
第二节分部积分法
在学习这节之前,我们需要掌握一个公式:
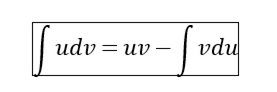
u,v是函数
(这个公式是利用链式求导法则的微分形式,然后在等号两边分别积分就得到的)
例1.假设要计算

令u=x并且dv=e^x dx ,这时就有

现在我们还需要找到du和v ,这样就可使用分部积分
du比较简单, du=dx (因为u=X ,所以du/dx=1 )
那v呢?我们只知道dv=e^x dx ,即dv/dx=e^x ,很明显那么v=e^x
现在就可以使用分部积分法了:
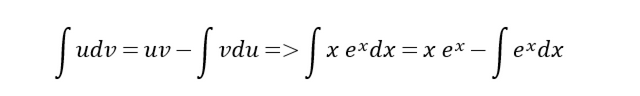
也就是

这就是答案
例2.求
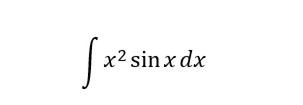
首先我们令u=x^ 2,dv=sinx dx
那么就有V= -cosx,du= 2x
然后使用分部积分法:
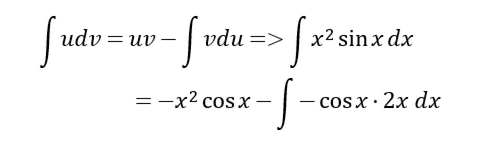
即
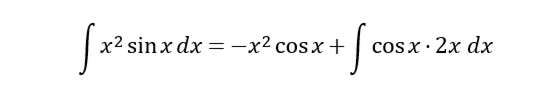
然后我们发现,等号右边的第一项貌似还要使用一次分部积分法
没错,的确是的
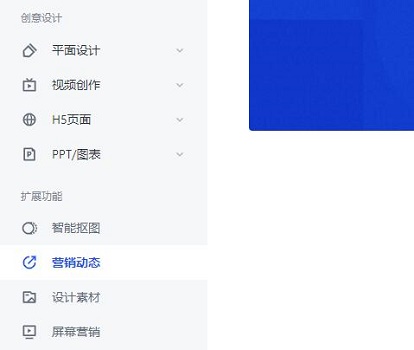
先把等号右边的第二项的2提出来,然后使用分部积分
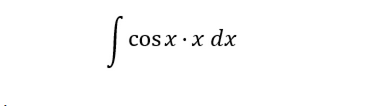
那么令U=x,dv=COsx dx
则V=-sinx, dU=dx
这样替代,就有:

即
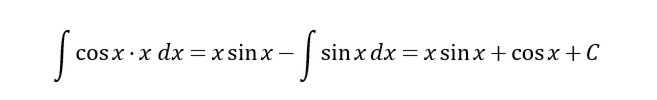
然后带入回去,即得到
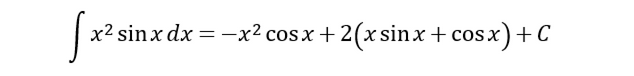
注意:这里的乘上2的,因为常数乘以常数还是常数e^(-x^2)的积分怎么求e^(-x^2)的积分怎么求,所以可以直接+C而不是+2C


限 时 特 惠: 本站每日持续更新海量各大内部创业教程,加站长微信免费获取积分,会员只需38元,全站资源免费下载 点击查看详情
站 长 微 信: thumbxmw

